Jacking force

[Z]

BUT...

I am a bit suspicious of using the skew parallelogram to calculate the control arm force. Yes it's a valid way of representing the resultant contact patch force, but you get a control arm force smaller than it should be. I have taken your same problem and decomposed the LH wheel force into n-t coords which is a recangular parallogram. I get a control arm force of 3.434kN (as opposed to your 3.015kN).

To represent it graphically, below on the right is how you have decomposed the contact patch force into n-z (normal,vertical) coords. On the left is how I did it using n-t (normal,tangent) coords.


The reason that your control arm force is smaller is because your Z (vertical) component contains a component acting along the n-axis. I think this is significant because in this example alone there is a 13% difference.

Tim,

Yes, you are 100% correct.

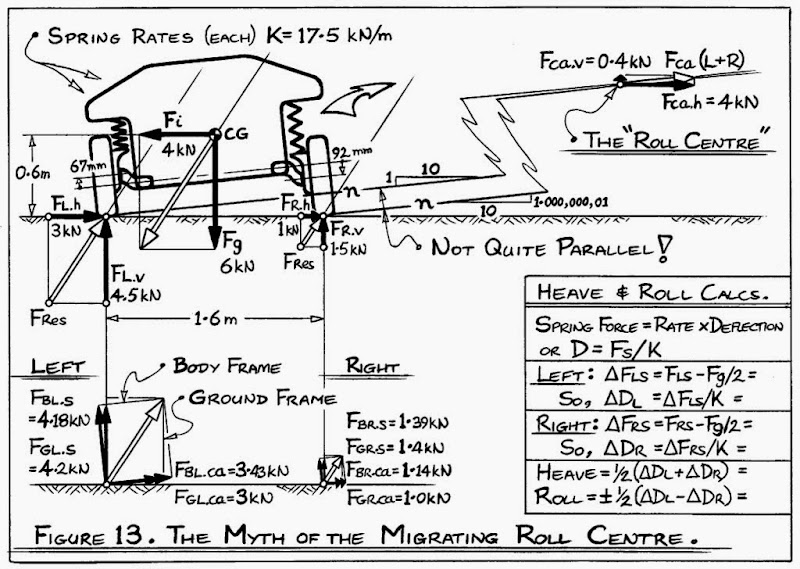
And, indeed, that is the way I had it on the original version of Figure 13 (shown below).



On the updated Figure 13 (several posts ago) I removed the body-reference-frame forces because I figured it was all getting a bit cluttered. Also, when looking just at the ground-frame force components, it is easy to see that the left wheelprint vertical force Fl.v = 4.5 kN (at top-left of sketch) equals the spring force Fgl.s = 4.2 kN, plus the control-arm vertical (jacking) component Fgl.ca x 1/10 = 0.3 kN (at bottom-left of sketch).

For control-arm stress calculations, decomposition of the forces in the body-frame is better. But, of course, any angularity of the real spring-damper (or its push/pull-rod) away from vertically above the wheelprint must also be factored into the calculations. As you have noted, a spring-damper that angles down-and-outward toward the wheelprint is beneficial in that it helps the control-arms by resisting some of the up-and-inward road-to-tyre loads.
~~~~~o0o~~~~~

As a further little twist, students might again consider the spring and control-arm forces in the body-frame (perhaps clearer in Tim's sketch, at left). The control-arm (or n-line) forces in this frame are horizontal wrt car-body-frame. Yet we should still expect the calculations for "jacking" effect to be the same as before, namely a Heave motion of about 12 mm. But horizontal n-lines CANNOT cause any jacking... So WT!!!???

The resolution to this problem comes from looking at the "body" forces Fg and Fi acting through the CG of the car. In particular, in the body-reference frame, Fg has a small leftward component, and Fi has a small UPWARD (!) component of ~0.4 kN, which, in effect, lifts the car ~12 mm

Z

[BillCobb]

(Sorry, I couldn't resist the title).

In the industry, jacking is a force AND moment issue requiring nonlinear 3D elastic analysis simply because there are now legal implications to doing it wrong. The jacking problem has its most pronounced appearance during incipient vehicle rollover. Thus the only sane measure is a derivative proof, because the mechanism represents an instability: Once the 2nd partial derivative of lateral acceleration by C.G. height goes awry, you have a rollover.

The forces on suspension members will generally climb well above normal durability requirements. Tire AND wheel stresses are sometimes beyond tire test machine capabilities (FWIW: I've posted a few TIRF tire test videos that have been questioned as to why so severe. The simple answer is that the tire tests were run based on load wheel and axle slip angle measurements of vehicle road tests where the vehicle(s) suffered from yaw instabilities, broke chassis and frame parts and flipped over. I may be able to resurrect some videos showing this treacherous condition. When round 5 spoke wheels come back looking like pentagons, you have to believe that jacking analysis and control is not to be taken lightly.

Another way to visualize this is with the simple but elegant SidePull Test. A cable fastened to the vehicle CG location while parked on a bedplate, pulls horizontally at all times until there is 2 wheel lift. Yes, the vehicle yaws, bends and twists. Yes, the CG height moves (especially upward during the test. Yes, the pulling winch must track the change in CG location so that the cable is always horizontal. Yes, you will see the enormous MX distortion. And unfortunately yes, the tire is not rolling. But: You quickly get convinced of this being a 3D event.

Also Yes, the Saturn Vue had to switch to Chevy Equinox rear LCAs as the original CAs broke during these events. This was because of the jacking MOMENTS during DYNAMIC roll events.

[Z]

During some recent discussions on this subject, it dawned on me that perhaps the best way that you students can get a deeper understanding of "Jacking Forces" is ..... the same way that I did many years ago.

Back when I was figuring this stuff out I started with a first-principles approach as outlined in the "Finding the Jacking Forces" post, back on page 4. But just because it seemed to make sense on paper did NOT quite convince me that it works like that in real life. Did I miss something? I had certainly cocked-up many times before! So I decided to test my figuring with a slightly more realistic 2-D Jacking Force Simulator, as sketched below.

I suggest all FSAE teams try something like this, because it gives an immediate "kinaesthetic" appreciation of the problem (ie. you poke it, and you instantly see and feel how it responds). It would be a good project for Newbie students, giving them some "how to make stuff" skills, plus, of course, getting them up-to-speed on some basic Vehicle Dynamics.
~o0o~

Briefly, the "ground-frame" is a sheet of ~10+ mm thick plywood about 1 metre square (or 2' to 3' square would do, or even use a tabletop). The "car-body" is to scale, and can be thinner plywood. The "control-arm-n-lines" can be similar plywood, or suitable flat metal bar. Strings represent various forces, and rubber bands (from local newsagent/office-supply store) make great suspension springs, and also more flexible forces (eg. gravity, which gives a roughly constant force regardless of position). All pieces are jointed together with ~30 mm long, ~M4 screws and nuts (I had a box full of them).

Total build time should be a few hours. For a prettier "educational tool", add a few coats of paint (primer+undercoat first!), with the "road surface", "force names", "CG", etc., labels added. If you really want to jazz it up, then add "fishing scales" to some of the strings to give quantitative force readings (only the 4 x wheelprint force components are needed...).



Some Notes.
==========
* As sketched, the "Simulator" shows an end-view of a car cornering to the right, so with centrifugal force (Fi) to the left. This particular car has adjustable L/R toe-angles which gives it variable slip-angle tyre forces (ie. the string tensions Fl.y and Fr.y can be controlled by your hands). (Or it might be a typical FSAE car with floppy toe linkages that move all over the place... ). Any angular "car-body" motion is thus Roll.

* Alternatively, you can see the Simulator as a side-view of a car, either accelerating rightward (it has variable torque-split 4WD), or moving leftward and braking with variable F/R bias (again, set by how hard you pull on the two strings). Now angular body motion is Pitch. In both cases any vertical motion of the car CG, wrt the ground-frame, is Heave, or "Jacking".

* The car-body unrealistically penetrates underground. This doesn't matter, because it is only a model! Doing it this way just makes it easier to use tension springs for the suspension (ie. the underground rubber bands, rather than compressive coils above the wheel), and the n-lines can easily be adjusted to slope down-to-centre.

* Like the upside-down suspension springs, the road is "pulling-up" on the wheelprints from above (ie. via the vertical Fz strings), rather than "pushing-up" from below. Again, no problems. In fact, doing it as shown may help with your understanding of the Axiom of Statics (page 4) that says that "forces are SLIDING vectors" (ie. they can act anywhere along their Lines-of-Action, always with the same effect). In general, using strings and rubber bands like this works great for any sort of force analysis, including 3-D problems.

* As noted before on this thread, for this particular problem it does NOT matter where along the n-line the swing-arm's pivot point, or IC, is located. If anyone doubts this, then they might try making a larger "car-body", which has n-lines with the same slope as in the sketch, but with the swing-arms pivoting outboard of the wheelprints and below ground. In these two different cases, the "instantaneous" behaviour (ie. amount of Heave and Roll/Pitch for given horizontal wheelprint forces) should be exactly the same. In fact, the only difference between inboard or outboard ICs is that as the body position changes significantly, the n-line slopes will change in different directions.

* Also as noted before, it should be apparent that the body does NOT rotate around the Roll (or Pitch) Centre! This should be immediately obvious if you set up the n-lines roughly as in the sketch. Pull with your left hand (Fl.y) and the body Heaves UP quite a lot, and Rolls a little anti-clockwise. Pull with your right hand (Fr.y) and the body Heaves DOWN a little, and Rolls anti-clockwise a lot more. If you factor in sliding of the wheelprints on the ground (as in the "Where is the Motion Centre?" sketch on the "Anti Dive Setup" thread), then the 2-D Motion Centre (ie. the IC of car-body wrt ground) is even further away.

* The above Simulator is roughly half-way between a pen-and-paper analysis, and the full-size, 3-D, real-deal. Obviously, full-size testing (as mentioned by Bill above, and in Doug's RCVD) is by far the most accurate, but it also takes quite a lot of time and money. Especially so, if you want to model lots of different n-line slopes and the like. Pen-and-paper is by far the cheapest, and lightning fast, BUT ONLY ACCURATE WHEN DONE RIGHT (which is rare these days, because it requires a good education system...). And it seems that computerised simulators have yet to catch up with pen-and-paper, given that I have yet to find a general purpose, easy-to-use, AND accurate, one.

So, some plywood, string, rubber-bands, screws, and a couple of hours of effort, in return for good understanding of Jacking Forces.

First to build, please post some pics (mine long ago dissappeared into a bonfire...).

Z

[Ahmad Rezq]

Tim Wright,
Correct me if I'am wrong.
The control arm force necessarily lie on the n-LINE but this doesn't mean that its the only force that lie on the n-LINE. for example if we take one side in a 2-D rear view of cornering Vehicle with double wishbone suspension (2-Links) so that they have horizontal n line wrt the ground, and direct acting spring damper pointed to the contact patch and leans for example 50 degrees with the horizontal. force analysis of this problem will give 3 forces (lower control arm force, upper control arm force, spring damper force). the resultant of the two control arms force will be directed along the n-LINE (i.e horizontal) and the spring damper force which is along the spring damper axis i.e 50 degrees with the horizontal can be decomposed into a component normal to n-line and a component along the n-line so the increase in the forces along the n-LINE IMO is because of the component of the spring damper force. if I'am correct and didn't miss something so the control arm forces will remain the same and the spring damper will help the control arms in this case.

[Tim.Wright]

Hi Ahmad,

What you say is more or less correct. Essentially you can also decompose the reaction forces at the spring into n-t coordinates in the same way that you do at the contact patch. This will tell you how much of the spring force is actually used in reacting the contact patch loads and how much is wasted by being reacted through the links. The more aligned the spring is to the 't' direction of its attachment point, the lower spring force you need to balance a given contact patch force.

So while it's true that the control arms forces contain 2 components (from the contact patch and from the spring) the important thing to remember is that the only component of that which affects the jacking beahviour is the one at the contact patch. The component from the spring only affects what spring rate you need to balance the reaction.

This is all part of a more general phenomonen which you see in any system where you have action and reaction forces which are misaligned with their respective degrees of freedom. If you consider the system below which could represent a swing arm (red), a vertical contact patch action (orange) and a spring reaction (blue) - you can see that for different position of the swingarm, you have a varying breakdown of the 'n' and 't' components of both the action and reaction forces. For example you can see in position '0', the action force is perfectly aligned with the vertical 't' direction of the swing arm but at positions 'R' and 'B' there is a misalignment which causes an 'n' component.


The interesting thing to come out of the study of a simple system like that is that if the reaction is a spring and the action is a force, then the equivalent stiffness at the point of application of the action force is NOT simply the spring stiffness multiplied by the motion ratio squared like the books and the seminars say. The variation of the misalignment of the action and reaction forces cause a variation in the motion ratio and this variation actually adds another component to the equivalent stiffness to the contact patch. You will see this in a proper multibody simulation on a suspension which has a progressive motion ratio whereby the actual wheel rate appears higher than that predicted by the formula Kwhl = Kspring x MR^2.

You can see this for yourself by doing a virtual work analysis on a hypothetical suspension which has a non constant motion ratio. The result is that the wheel rate is equal to:
Kwhl = Kspring x MR^2 + Fspring x dMR/dz,
where dMR/dz is the slope of the motion ratio curve with wheel centre vertical travel and Fspring is the force in the spring at any instant.

This extra component can vary between zero (if your motion ratios are perfectly constant) to >20% (in the case of a highly non linear motion ratio often seen in racing MacPherson suspensions) of the real wheel rate. Its often around 10-15% for a direct acting double wishbone suspension. So it's far from negligible.

Tim

[Claude Rouelle]

There are jacking forces that most of students do not take into account and that could make a significant difference in thee steady state ride heights calculation (skid pad)
- Jacking forces due to the tire Mx (overturning moment) they do not have the same value and most of the time the same sign either on the inside and outside wheel
- Jacking forces due to the side load applied at the non suspended mass CG (yes, these non suspended masses do "see:" some lateral G too) and the difference of altitude between the non-suspended mass CG and this non suspended mass instant center. Could be non negligible
- Jacking forces due to the tire side load (horizontal force applied on the tire contact patch) and the difference between the contact patch altitude (z = 0) and the instant center altitude.

[Tim.Wright]

I think the main source of error in calculating the overall jacking force of an axle comes from the unknown distribution of the lateral cornering forces between left and right as its indeterminate.

[Claude Rouelle]

Yep and that is why a tire model helps. No tire model is perfect but it helps to narrow the gap between simulation and reality

[BillCobb]

Given a whole set of tire data and a manageable way to present and use it, one can show (Even in 2D) what you are faced with as far as Mx influences on a suspension. So let's say we were given a Pacejka-Lite (4 terms) tire function and some theoretical parameters for a no-special or distinct or specific tire at some typical usage pressure on a common rim width, one could quickly examine the complicated effects that a pair of tires are having on your jack donkey. I'd bet that it's its more a structural durability issue on a FSAE car instead of what it means to Production Vehicle engineering (specifically SUVs and trucks).

That being said, all you folks wanting to get the most bang for your dinars will want to study the overturning moment responses specifically at various camber angles (as in Optimization of camber on the wheels of each axle as a function of lateral acceleration). Wheew, don't spill any brew trying to read that outloud... Best to fit Fy and Mx as a function of (SA, FZ, IA) and sort it out with a constant radius sim. Keeping the tread under the wheel rim will keep your car from being 'snap loose' (as in tight but "it speened out without a hint"). That would also be referred to "tighty loose" as Terry Satchell would say.

BTW: This simple tire model seems to replicate real TTC data VERY well. I'll put my .m scripts on the TTC forum so you can blast away on real data.

[BillCobb]

Well they used ADAMS and all the wizzbang stuff but left out the OVTM stuff and here's what you get (see the pic): Broken parts. Then you go to TIRF and get the real stuff (ref. video).

https://www.youtube.com/watch?v=nmo_dkNZIHM

You can get an award for helping to fix this: