Sid@TR,
Some comments on your "ROLE OF A ROLL CENTER (Mystery solved or mystery continues?)".
~~~o0o~~~
"Basic definition of roll center is the point about which the sprung mass rolls under the influence of centrifugal force."
This "RC = Motion Centre" definition is perhaps the worst of the many definitions of RCs. Mainly because it does NOT take into account any vertical (= jacking!) motion of the sprung mass, or lateral sliding of the wheels on the ground. I would avoid using it.
~~~o0o~~~
"It is also a point through which the lateral forces transmitted from Tire’s contact patch acts upon achassis."
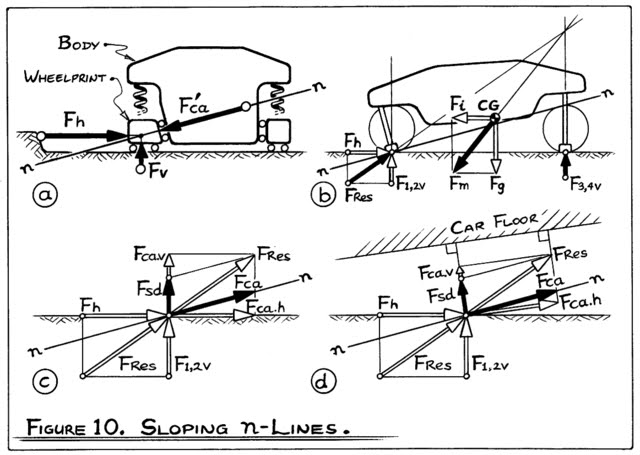
... together with the jacking forces! It is the point (in this simplified 2-D example) where the "control-arm forces" from both wheelprints, acting along their respective n-lines, can be vectorially combined into a single force acting on the body. In general this force will NOT be purely horizontal.
IMPORTANT NOTE (to restress above). Each control-arm force is, in general, NOT horizontal, because its n-line is not horizontal. So, since the control-arm force has horizontal Fy, and vertical Fjacking, components, BOTH of these must be moved to the RC. That is, each resultant control-arm force (Fr.ca or Fl.ca in previous posts) is SLID along its LoA (= the n-line) to the RC, carrying its two components, Fy & Fj, with it.
Less important note. RCs, namely the intersection point of the two lateral n-lines, frequently zoom off to infinity (or at least out past Pluto...). This happens with any suspension with that has n-lines that remain notionally horizontal wrt the body (= ~ ground level RC), and the body then adopts a roll angle (ie. because parallel lines meet at infinity). There is NOTHING WRONG with these suspensions. They are common, and well behaved. But your computer won't be able to do the calculations for "roll moments due to the forces at the RC" because the numbers are tooooo big!
BTW, the above bold print is a reasonable definition of "the RC".
~~~o0o~~~
"6. Concepts given in “Suspension Geometry And Computation” by J.C.Dixon"
I have Dixon's book "Tires, Suspension and Handling.", but nothing with the above name. Is that a paper?
I have fewer notes in the margins of Dixon's book that in most others (ie. it is "less wrong"). IMO, Chapter 5 "Suspension Characteristics" is better than most other books on this subject.
~~~o0o~~~
"Steps-
1. Draw vector Fg + Fi=R from COG. Here, Fg=mg i.e. weight and Fi is the inertial force.
2. Assume/get the coefficient of friction of one tire."
There are many ways of taking this step (2), some of which I covered at the top of page 3. Briefly, for equilibrium the wheelprint forces Fl and Fr MUST intersect somewhere along Fg+i's LoA (your "R"). So you can pick, or assume, ANY point along this LOA, and then all results are found.
A good first approximation is to assume that both tyres have the same CoF, so Fl and Fr are parallel to each other, and also to Fg+i (ie. they all intersect "at infinity"). Note, however, that different toe angles, say from "Ackermann" at the front, can greatly affect whether the intersection point is above or below the car.
~~~o0o~~~
"8. Now, resolve Fl and Fr along and perpendicular to n-line-fig(b)
9. Let Fl.ca be the force along n-line and Fl.sd be the force perpendicular to n-line."
Having the control-arm (F.ca) and "virtual" spring-damper (F.sd) forces perpendicular is how Dixon does it, and is perfectly acceptable.
I prefer to have the F.sd force always vertical (wrt body) so that it represents the "virtual wheel-spring-damper-rate" (ie. one that is always vertically above the wheelprint).
IMPORTANT NOTE. When forces are "decomposed", the "components" do NOT have to be perpendicular. They can be at any angle that suits you. That is why the Parallelogram Rule is not called the Rectangle Rule.
For a given total wheelprint force, say Fl, changing the angle of Fl.sd will change the magnitude of Fl.ca. Likewise, changing the angle of a real spring-damper (or pushrod) will change the loads on real control arms. However, for the vertical wheel-rate to remain as before, the newly positioned spring-damper must also have a different rate spring (stiffer or softer). If this is done, then the body roll in corners will be as before, even though the control-arms and spring-damper are differently stressed. This better understood by working through numerous examples...
~~~o0o~~~
"10. Now, consider Fl.ca and Fr.ca. Resolve them into horizontal and vertical component namely Fl.ca.y and Fl.ca.j similarly with right side-fig(d)
11. Net jacking force=Fl.ca.j-Fr.ca."
Strictly speaking, net jacking force = Fl.ca.j + Fr.ca.j (Fr.ca.j has negative magnitude in the sketch).
As I said before, VW Beetles can have their tails jump upwards so much from these forces that both rear wheels leave the ground.
~~~o0o~~~
"CONCLUSION
...
2. Roll center migration should not be a headache because unless the jacking force is undercontrol (if you want so) the roll center migration is irrelevant.
3. The more the inclination of n-line, the more will be the jacking force. So migration of n-lineshould be controlled."
Yes. I suggest you aim for n-line slopes close to horizontal (say, less than 10 degrees up or down), and not suddenly changing their angle, wrt body, with small movements of the suspension.
Another way of saying this same thing, is that the centre-of-wheelprint's "path of motion" should be a straightish line (gentle curve is acceptable) that is close to vertical.
~~~o0o~~~
"DOUBTS
1. In this concept, what constitues a roll couple? Which force acts along with the Centrifugal force and what is the moment arm in this case?"
All force diagrams (that use D'Alembert's Principle) ultimately result in zero force (ie. equilibrium)! Along the way you can arrange the forces in many ways, some of which represent "roll couples" acting on the "sprung mass". One way to do this was touched on above. Namely, slide both Fl.ca and Fr.ca to the RC. Next decompose the resultant of these two into horizontal (Fca.h = Fl.ca.y+Fr.ca.y), and vertical (Fca.v = Fl.ca.j+Fr.ca.j) components.
The couple formed by Fca.h, at RC height, and the centrifugal force Fi, at CG height, typically acts to roll the body outwards during cornering. This couple is resisted by (equilibriated by) a couple formed from changes to the vertical spring forces, namely delta.Fl.sd and delta.Fr.sd. This explains why cars with high RCs, and thus lesser CG-RC "moment arm", roll less than ones with low RCs, all else equal.
The couple formed by the jacking forces Fca.v, at the RC, and a component of the weight force Fg, at the CG (assuming that the RC is not directly under CG), is typically ignored by many people, such as Danny! Including this couple will correct Danny's earlier calculations with RCs, and give the same results as his FAPs. (Edit: Note that this "correction couple" is small when the RC is near the CG, but it is astronomically large when the RC is out near Pluto...) The fact that this couple includes a part of Fg means that Fg is now "diminished", so lesser spring forces are required to carry it. So the car "jacks up", which is also all too often ignored.
~~~o0o~~~
"5. Why in Tune To Win, Carroll Smith has entirely a different approach?"
The section on jacking (page 38) and Figure 18 (p39) is reasonably accurate IMO, and similar to what I have been saying here. (The Figure has some small errors, and could do with more arrows and explanation.) However, some other parts of the book might be taken with a large grain of salt...
Carroll, a largely self-taught race engineer, includes this statement in the Preface (and in most of his other books).
"I am fully aware that much of what I have to say is subjective...
I wish that my knowledge and wisdom were such that this were not so....
I will put forth my personal best shot on the subject at the time of writing.
I reserve my right to change my thinking at any time."
And, indeed, Carroll often did change his thinking when he came upon better explanations.
~~~o0o~~~
"6. So many concepts, which one to follow? Or more specifically, which one is more closer to reality?"
I stress again that the explanation I gave above (post with sketch) is a greatly simplified version of "reality". (Even in 2-D it doesn't include "roll acceleration". This adds an "inertial couple" to the sketch, and changes all the forces quite a bit. Though also easy enough to understand...)
However, the concepts in Euclid's Elements, Newton's Principia, and all the rest of Classical Mechanics, is a good enough approximation of reality to have taken man to the Moon, and beyond! With that track record, and up against the alternatives from the automotive/motorsport cottage industries, I know which one I choose.
Z

|
|



 Reply With Quote
Reply With Quote


 ). I will try again tomorrow...
). I will try again tomorrow...

